Олимпиада

(Подготовка к участию в окружном туре Всероссийской олимпиады по информатике для 6 класса)

Большая часть олимпиадных заданий основана на рассуждениях с использованием чисел.
Для успешного выполнения надо знать методы решения для стандартных ситуаций и способы рациональных действий. Они очень пригодятся при последующей учебе и в жизни.
1. Табличный способ решения задач.
2. Графы, дерево решений.
3. Закономерности рассуждений с четностью чисел.
4. Способы быстрых вычислений, признаки делимости чисел.
5. Закономерности в рядах.
6. "Рисование" невозможного (проведи 1000 линий...).
7. Умение кодировать объекты из задания для краткой записи решения.
Нужно знать степени числа 2 и числительные приставки количества информации.
Сколько может...
...

Окружная олимпиада: 2009, 2010, 2011

Школьная олимпиада: 2010,

Задачи

+ стоит перед обсужденными (++) или заданными на дом (+) задачами
* — перед реальными олимпиадными задачами.

++а) Чем кончается день и ночь? б) Чем кончается лето и начинается осень?
+В клетке находятся четыре крысы. Четыре девочки попросили дать им по одной крысе, что и было сделано. Но в клетке осталась одна крыса. Как это могло произойти?
+По улице идут два сына и два отца. Всего три человека. Может ли такое произойти?
+*Три гнома хотят перевезти 20 рубинов и 9 изумрудов из Глубоких Шахт в Великий Тайник за один рейс. Как им разложить камни по трем тележкам, если грузоподъемность каждой тележки 44 кг, вес каждого рубина 3 кг, а вес каждого изумруда 8 кг?
+Одному пожилому человеку 100 лет, но день рождения он мог отпраздновать намного меньше, чем 100 раз. Сколько и почему?
Найди лишнее число в ряду:
++а) 2, 3, 6, 7, 11;
++б) 18, 12, 3, 29, 45, 28;
+в) 10, 20, 30, 36, 40, 50;
+г) 72, 62, 52, 45, 32, 82;
+д) 24, 29, 22, 37, 25, 28.
+Продолжите ряд (3 буквы): П, В, Т, Ч, П, Ш.
+В каком порядке выстроены цифры: 8, 2, 9, 0, 1, 5, 7, 3, 4, 6.
+Допишите одно число в ряду: 77, 49, 36, 18, ...
Продолжите ряд (не менее четырех значений):
++а) 1, 10, 3, 9, 5, 8, 7, 7, 9, 6;
+б) 16, 12, 15, 11, 14, 10;
+в) б, а, в, б, г, в, д, г, е;
+г) 1, 3, 2, 2, 5, 4, 3, 7, 6, 4, 9, 8.
Допишите по два числа в начало и конец ряда:
++а) ..., 5, 7, 9, ...;
+б) ..., 5, 6, 9, 10, ...;
+в) ..., 21, 17, 13, ...;
Завершите ряд соответствий: 4→61, 5→52, 6→63, 7→94, 8→46, 9→...
Продолжите последовательность: 8, 6, 10, 6, 12, 6...
Чему равна сумма чисел: а) первой сотни ; б) первой тысячи.
*На столе стоят пять коробок. В первой одна бусинка, во второй — две, в третьей — три, в четвертой — четыре и в пятой — пять. Первым ходом можно положить в любую коробку или вытащить из нее 1 бусинку или пропустить ход (ничего не изменять), вторым — положить или вытащить 2 бусинки (из той же или другой коробки) или пропустить ход, третьим — 3 или пропустить ход, и так далее. Требуется за несколько ходов сделать так, чтобы в каждой коробке было по 20 бусинок.
++а) Опишите последовательность действий на каждом шаге, приводящей к решению поставленной задачи (не обязательно за минимальное количество ходов).
+б) Решите предыдущую задачу, если пропускать ходы не разрешается.
*Исполнитель стоит на клетчатом поле. Исполнитель может выполнять команды вправо, влево, вверх, вниз. При выполнении любой из этих команд исполнитель перемещается на одну клетку соответственно вправо →, влево ←, вверх ↑, вниз ↓ по полю. Все клетки, через которые проходит исполнитель (включая начальную и конечную), он помечает. Дана программа для этого исполнителя:
```
	НАЧАЛО
		ПОВТОРИТЬ 100 РАЗ
		  вправо
		  вправо
		  влево
		  влево
		  вверх
		  вправо
		  вниз
		КОНЕЦ
	КОНЕЦ
	
```
Сколько клеток будет помечено в результате выполнения этой программы? Ответ обоснуйте.
Примечание. Если через какую-то клетку исполнитель проходит несколько раз, при подсчете числа помеченных клеток ее нужно учитывать один раз.
*Петя, Вася, Маша и Аня пришли в кафе позавтракать. Завтрак каждого из них должен состоять из одного горячего блюда и одного напитка.
Меню кафе выглядит так:

Горячие блюда Напитки

Каша — 40 руб. Чай — 5 руб.

Омлет — 50 руб. Какао — 20 руб.

Блинчики — 60 руб. Кофе — 30 руб..

При этом в кафе действует акция — если друзья заказывают три одинаковых блюда (например, три чая), то они платят только за два, а третье получают в подарок. Если же они заказывают одно, два или четыре блюда, то платят, как за одно, два и три блюда соответственно.
Известно, что Петя с утра пьет только кофе, и предпочитает блинчики. Вася хочет либо кофе и омлет, либо чай и блинчики. Маша не ест кашу и хочет попробовать какао. Аня хочет омлет и не пьет какао.
Кто и что должен заказать, чтобы в сумме ребята заплатили как можно меньше, и все пожелания оказались учтены? Сколько они в итоге за все заплатят? Объясните, почему при этом стоимость действительно окажется минимальной.

*Вася записывает на доске последовательности чисел. Первая последовательность состоит из одного числа, а каждая следующая описывает предыдущую так, как это показано ниже.

№	Последовательность	Как читать последовательность (слова в описании соответствуют числам текущей последовательности слева направо, и описывают предыдущую последовательность)
1	2	Исходная последовательность
2	1 2	Одна «двойка»
3	1 1 1 2	Одна «единица», одна «двойка»
4	3 1 1 2	Три «единицы», одна «двойка»
5	1 3 2 1 1 2	Одна «тройка», две «единицы», одна «двойка»
6	1 1 1 3 1 2 2 1 1 2	Одна «единица», одна «тройка», одна «двойка», две «единицы», одна «двойка»

Выпишите последовательность, которую Вася напишет на 10-ом шаге.

Сколько потребуется времени, чтобы поезд длиной 1 км, идущий со скоростью 60 км/час, прошел тонель длиной в 1 км? (Очень важно дать ответ на вопрос: где подвох и в каком количестве он выражается?)
+Как найти сумму чисел рациональным способом? (есть несколько решений)
7 + 10 + 13 + 16 + 19 + 22 + 25 + 28.
+В квадрате 3×3 клетки расставьте числа от 1 до 9 так, чтобы их сумма в каждой строке, столбце и диагонали была одинаковая.
+В квадрате 3×3 клетки расставьте числа от 0 до 8 так, чтобы их сумма в каждой строке, столбце и диагонали была одинаковая.
Припишите к числу 10 по одной цифре слева и справа, чтобы полученное число делилось на 72.
Во сколько раз путь на 10-й этаж длинее, чем на 2-й?
Сколько раз встречается цифра 7 в записи чисел от 1 до 100?
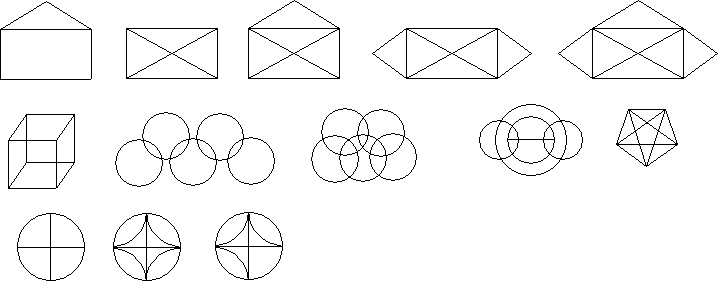
Найдите рисунки, которые нельзя нарисовать не отрывая руки или не проводя линию дважды. Для остальных — укажите возможные точки начала рисования.
100 человек пожали друг другу руки. Сколько всего было рукопожатий?
Какими наборами чисел (кроме просто натурального ряда) можно получить любое целое число при сложении?
В семье три сестры. Каждая из них на 4 года старше предыдущей. Сумма их возрастов равна 27. Сколько лет каждой из них?
На шахматной доске 8*8 всего 64 клетки: 32 белых и 32 черных. а) Сколько еще квадратов размером от 2*2 клетки можно найти на доске? б) Сколько среди них квадратов с одинаковым числом черных и белых клеток?
Продолжи числовой ряд. а) 1, 6, 11, 4, 9, ... б) 1, 12, 10, 7, 3, ...
Заполните магический квадрат до конца годами последних двух десятилетий XX в.

1994

1991
2013 год начинается во вторник. В какой день недели начинается 2114 год.
5 человек пожали друг другу руки. Сколько всего было рукопожатий?
Нужно определить день и месяц рождения человека. Он честно ответит на любой вопрос "да" или "нет".
0. Объясните, как вы собираетесь считать. Если не знаете, то это будет почти гаданием. Попробуйте отгадать.
1. Сколько вопросов потребуется задать? (Подсказка: их намного меньше 20.)
2. Сформулируйте эти вопросы. (Только этот вопрос требует более 10 секунд на ответ.)
3. Сколько вопросов добавится, если выяснять год рождения? (Подсказка: рекорд долгожительства - 131 полный год.)
Сколько существует трехзначных чисел, все цифры которых нечетные и никакие цифры не повторяются внутри числа?
Человек отвечает на вопросы только "да" или "нет" и имеет право соврать только один раз. Посреди вопросов его спросили: "Ты соврал?", и он ответил: "Нет". Может ли он врать в дальнейшем? (Это задание является ключевым на составление вопросов с правдивым ответом.)
В мешке лежат 5 белых и 2 черных шара.
а) Сколько шаров надо вытащить из мешка, чтобы среди них оказался хотя бы один белый?
б) -"- хотя бы один черный?
в) -"- хотя бы один белый и хотя бы один черный?
г) -"-, чтобы среди них наверняка оказались 3 белых и 1 черный шар?
г) -"-, чтобы среди них 2 шара одного цвета?
В мешке лежат 100 шаров трех цветов. Сколько шаров надо вытащить, чтобы среди них оказалось 30 шаров одного цвета?
а) Есть три ключа от трех дверей с разными замками. Достаточно ли трех проб, чтобы подобрать ключи к к дверям?
б) Есть пять ключей от пяти комнат с разными замками. Сколько потребуется проб в худшем случае, чтобы подобрать ключи к комнатам? в) Есть 100 ключей от 100 комнат с разными замками. Сколько потребуется проб в худшем случае, чтобы подобрать ключи к комнатам?
Иван-царевич добыл ключи от нескольких комнат в подземелье, но не знал, какой ключ от какой комнаты. Сколько комнат в подземелье, если в худшем случае ему достаточно 21 пробы, чтобы выяснить, какой ключ от какой комнаты?
Один мальчик сказал: "У меня 24 пальца. На каждой руке по пять, а на ногах — 12". Как это может быть?
Как разложить 333 монеты достоинством в 1 рубль на 9 мешочков так, чтобы ими можно было набрать любую сумму от 1 до 333 рублей?
Продолжи числовой ряд: 1, 2, 4, 8, 16... Чему равна сумма: а) 10 чисел этого ряда? б) 16 чисел этого ряда?

Чертежник выполнил программу:

	повтори 4 раз
		сместиться на (-1, -3)
		сместиться на (3, 0)
		сместиться на (-1, 3)
	конец
	сместиться на (-3, -2)

Какую команду он должен выполнить, чтобы вернуться в исходную точку?

Чертежник выполнил программу:

	сместиться на (-4, -1)
	повтори 3 раз
		сместиться на (-5, -1)
		сместиться на (3, 2)
		сместиться на (3, -1)
	конец

Какую команду он должен выполнить, чтобы вернуться в исходную точку?

Робот находится в левом верхнем углу прямоугольной области неизвестного размера, со всех сторон окруженной стенками. Посередине находится стена, в которой есть проход. Где он, точно неизвестно, но проход не примыкает к нижней стенке. Задача: написать программу, которая переведет робота в правый нижний угол.
Напишите для Чертежника программу рисования буквы "У" так, чтобы её можно было получить в любом месте координатной плоскости. Исполнителя переведите в позицию для написания следующей буквы.
Общие условия: высота буквы 4 клетки, ширина — 2 клетки.
Робот находится в лабиринте и выполняет программу:
```
	НАЧАЛО
		ПОКА справа свободно вправо
		ПОКА снизу свободно вниз
		ПОКА слева свободно влево
		ПОКА сверху свободно вверх
	КОНЕЦ
	
```
Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?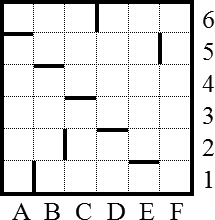
Робот находится в лабиринте и выполняет программу:
```
	НАЧАЛО
		ПОКА справа свободно вниз
		ПОКА снизу свободно влево
		ПОКА слева свободно вверх
		ПОКА сверху свободно вправо
	КОНЕЦ
	
```
Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?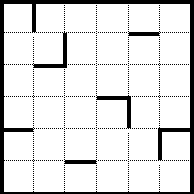
За сколько вопросов с ответом "да" или "нет" можно определить любое число a) от 1 до 11; б) от 1 до 1111?
В некоторой стране проживает 1000 человек. Индивидуальные номера налогоплательщиков (ИНН) содержат только цифры 0, 1, 2 и 3. Какова должна быть минимальная длина ИНН, если все жители имеют разные номера?
На пруду растет одна лилия. Каждый день число лилий удваивается. Весь пруд покрылся цветами на 10-й день.
Сколько выросло лилий? Сколько дней нужно для заполнения половины пруда?
Каким числом гирь можно взвесить любой груз до 63 кг, помещая их на одну чашку весов? Перечислите эти гири.
Какими тремя гирями можно взвесить груз до 13 кг включительно, если можно помещать их на любую чашку весов?
Какое минимальное основание имеет система счисления, в которой записаны числа 312, 123, 115, 321?
У меня 100 братьев. Младшему 1000 лет, а старшему 1111 лет. Старший учится в 1001 классе. Может ли такое быть?
Упорядочить числа по убыванию: 143₆; 50₉; 1222₃; 1011₄; 110011₂; 123₈.
В классе 1000_q учеников. Из них 120_q девочек и 110_q мальчиков. В какой системе счисления приведены значения?
В саду 88_q фруктовых деревьев, из них 32_q яблони, 22_q груши, 16_q слив и 17_q вишен. В какой системе счисления посчитаны деревья?
Восстановите неизвестные цифры, определив систему счисления:
а) 2?21 + 123? = ?203
б) 5?55 + ?327 = ?16?4
в) 21?02+ ?1212 = ?2?021
г) 4?5 — 136 = ?56
д) 1536 — ?42 = 674
Продолжи до конца числовой ряд (связанный с числом 16) в неизвестной системе счисления:
10, 11, 12, 13, 14, 15, 16, 17, 20, 22, 24...
В семье 4 сына: Вася, Миша, Коля, Петя. Им 5, 8, 16 и 15 лет. Определи возраст каждого из них, если один мальчик ходит в детский сад, Вася старше Миши, а сумма лет Васи и Коли делится на 3.
Исполнитель Вычислитель умеет выполнять 2 команды, приведенные ниже. Запишите программу его действий, при которой из числа a получится число b (a→b).
а) *2 и +1. 1→5; 1→50; 1→99
б) +3 и -1. 2→7; 1→15
в) *7 и +2. 1→29; 2→50
Исполнитель Вычислитель умеет выполнять 2 команды, приведенные ниже. Запишите программу его действий, содержащую не более 5 шагов, при которой из числа a получится число b (a→b). В ответе запишите номера команд (подряд, без разделения, например: 12211).
а) 1) *3 и 2) -1. 1→23
б) 1) *2 и 2) +1. 2→14
в) 1) ^2 и 2) -2. 1→49
г) 1) ^2 и 2) -3. 1→19
д) 1) *3 и 2) -5. 1→7
е) 1) *2 и 2) -4. 2→24
ж) 1) +3 и 2) *2. 1→25; 4→29
з) 1) *2 и 2) -5. 3→9
Сумма цифр двузначного числа, сложенная с их произведением равна самому числу. Запишите все возможные варианты числа.
Номер автомобиля состоит их трех букв русского алфавита (используется 29 букв) и четырех цифр (н-р, а1243бв). а) Сколько существует различных номеров? б) Сколько существует различных номеров, если используются только 12 букв, похожих по начертанию на латинские (АВЕКМНОРСТУХ)? в) На сколько уменьшится количество номеров в а) и б), если в номере не используется четыре нуля подряд?
Робот находится в левом верхнем углу прямоугольной области неизвестного размера, со всех сторон окруженной стенками. Посередине находится стена, в которой есть проход, шириной в 1 клетку. Где он, точно неизвестно. Задача: написать программу, которая переведет робота в правый нижний угол.
Робот находится в левом верхнем углу прямоугольной области неизвестного размера, со всех сторон окруженной стенками. Посередине находится стена, в которой есть проход, шириной не более, чем в 2 клетки. Где он, точно неизвестно. Задача: написать программу, которая переведет робота в правый нижний угол.
В классе учится 37 человек. Докажите, что среди них обязательно найдутся 4 человека, родившиеся в один и тот же месяц.
В классе учится 30 человек. Докажите, что среди них обязательно найдется пара, родившиеся в один и тот же день месяца.
В книге было написано 100 следующих утверждений:
"В этой книге ровно 1 неверное утверждение"
"В этой книге ровно 2 неверных утверждения"
...
"В этой книге ровно 100 неверных утверждений"
Какое из этих утверждений верное?
На острове живут рыцари, лжецы и хитрецы (слуги). Рыцари всегда говорят правду, лжецы всегда лгут, а хитрецы (слуги) говорят попеременно: то правду, то лгут.
Трое жителей (А, Б и В) разговаривали между собой в саду. Проходивший мимо незнакомец спросил у А: "Вы рыцарь или лжец?" Тот ответил, но неразборчиво. Тогда незнакомец спросил у Б: "Что сказал А?" "А сказал, что он лжец", - ответил Б. "Не верьте Б! Он лжет!" - вмешался в разговор В. Кем являются Б и В (из рыцарей и лжецов)?
В городе А живут рыцари, а в Б - лжецы. Прохожий встретил островитянина на дороге между городами. Какой вопрос он задал, чтобы узнать, где какой город? (См. №73)
Путешественнник нанял проводника-островитянина. При встрече с местным жителем, путешественнник послал проводника узнать, кем тот является. Проводник вернулся и сказал: "Рыцарь". Кем был проводник?
Произошел пожар. Дежурному пришло сообщение от неизвестного: "Пожар - в нашем квартале, где живут хитрецы". Куда должна ехать пожарная машина: к рыцарям, лжецам или хитрецам?
Три мальчика нашли древний кувшин и высказали свои мнения:
1-й: "Кувшин греческий и изготовлен в III веке".
2-й: "Кувшин турецкий и изготовлен во II веке".
3-й: "Кувшин не греческий и изготовлен в I веке".
Археолог сказал, что у каждого верно только одно предположение. Где и когда изготовлен кувшин?
Вася, Олег и Петя играли во дворе, и один из них разбил мячом окно. Вася сказал: "Это не я разбил". Олег сказал: "Это Петя разбил". Позднее выяснилось, что один сказал правду, а другой солгал. Кто разбил окно?
Сколькими способами можно разменять 50 копеек монетами в 1, 5 и 10 копеек? (Подсказка: их не так много. Можно попробовать построить дерево и выписать их все математически, например, 5*10, 4*10+2*5.)
Житель острова Крит говорит: "Все критяне - лжецы". Истинно или ложно это утверждение?
Дело происходило на острове, где живут рыцари и лжецы. Человек говорит: "Я лжец". Является ли он жителем острова?
На острове рыцарей и лжецов разговаривают А и Б. А говорит: "По крайней мере один из нас лжец". Что можно сказать об А и Б.
На площади собрались рыцари и лжецы. Каждый из собравшихся сказал: "Все вы лжецы". Сколько среди них рыцарей?
За круглым столом 7 жителей острова рыцарей и лжецов. Каждый из сидящих сказал: "Мои соседи - лжец и рыцарь". Кто сидит за столом?
За круглым столом 12 жителей острова рыцарей и лжецов. Каждый из них видит всех, за исключением своих соседей и, конечно, себя. Каждый из сидящих сказал: "Все, кого я вижу, - лжецы". Сколько рыцарей сидит за столом?
А и Б - жители острова рыцарей и лжецов. А говорит: "Я лжец, а Б не лжец". Кто из них рыцарь, а кто - лжец?
А, Б и В - жители острова рыцарей и лжецов. Двое из них говорят: А: "Мы все лжецы"; Б: "Один из нас рыцарь". Кто из них рыцарь, а кто - лжец?
А, Б и В - жители острова рыцарей и лжецов. Двое из них говорят: А: "Мы все лжецы"; Б: "Ровно один из нас лжец". Кем является В?
На острове всего два города. В одном живут рыцари, а в другом - лжецы. Встретились три человека. А говорит: "Б лжец". Б говорит: "А и В из одного города". Кто такой В?
На острове всего два города. В одном живут рыцари, а в другом - лжецы. Встретились три человека. А говорит: "Б лжец". Б говорит: "А и В из разных городов". В говорит: "А рыцарь". Кто есть кто?
А, Б, В, Г - жители острова лжецов. А говорит: "По меньшей мере один из нас лжец". Б говорит: "По меньшей мере двое из нас лжецы". В говорит: "По меньшей мере трое из нас лжецы". Г говорит: "Среди нас нет лжецов". Кто есть кто?
На острове лжецов совершено преступление. К суду привлечены трое. На вопрос судьи А ответил неразборчиво. Когда судья переспросил двух других, то Б сказал, что А утверждает, что он рыцарь, а В сказал, что А назвал себя лжецом. Кто есть кто?
В правительстве острова лжецов 12 министров.
Первый министр сказал: "Среди нас нет ни одного рыцаря".
Второй министр сказал: "Среди нас не более одного рыцаря".
И так далее до 12-го министра который сказал: "Среди нас не более одиннадцати рыцарей".
Сколько лжецов среди министров?
На острове лжецов живет 100 человек. Каждый житель поклоняется одному из богов: богу Солнца, богу Луны или богу Земли. Каждому жителю острова задали три вопроса:
1) поклоняетесь ли вы богу Солнца;
2) поклоняетесь ли вы богу Луны;
3) поклоняетесь ли вы богу Земли?
На первый вопрос утвердительно ответили 60 человек, на второй - 40 и на третий - 30. Сколько лжецов на острове?
За круглым столом сидят 2001 человек - рыцари и хитрецы. Каждый сидящий сказал: "Один из моих соседей - рыцарь, а другой - хитрец". Какое наибольшее количество рыцарей может сидеть за этим столом?
Три человека - рыцарь, лжец и хитрец - разговаривают. А: "Я хитрец". Б: "Это правда". С : "Я не хитрец". Кто они?
А и Б - жители острова рыцарей и лжецов - разговаривают. А: "Б рыцарь". Б: "А не рыцарь". Докажите, что по меньшей мере один из них говорит правду и является хитрецом.
А, Б и В - жители острова рыцарей, лжецов и хитрецов. Кто-то из них совершил преступление. А: "Я не делал этого, Б не делал этого". Б: "А не делал этого, В сделал это". С: "Я не делал этого, А сделал это".
Было установлено, что один из них дважды солгал, другой дважды сказал правду, а третий об одном человеке солгал, о другом сказал правду. Кто же преступник?
В забеге участвовали Костя, Илья, Дима и Миша. У каждого из них спросили, какое место он занял и они ответили.
Костя: "Я был последним".
Миша: "Я не был последним".
Илья: "Я был первым".
Дима: "Я не был ни первым, ни последним".
Оказалось, что трое сказали правду, а один солгал. Кто победил в забеге?
Числа 2146, 1991 и 1805 дают равные остатки при делении на натуральное число n, большее 1. Найдите n.
Анаграмма — слово (выражение), получаемое путем перестановки букв другого слова (выражения). Например, мол-лом.
Сколько анаграмм можно составить из сочетания букв "абвгд" (составлять их не надо, важно оценить сложность работы, которая дается ученикам первого класса).
Сколько анаграмм можно составить из сочетания букв "абвгде" (составлять их не надо, важно оценить сложность работы, которая дается ученикам второго класса).
Сколько анаграмм можно составить из сочетания букв "аабвг" (составлять их не надо).
Сколько анаграмм можно составить из сочетания букв "ааабв" (составлять их не надо).
Составьте анаграммы так, чтобы получились слова, имеющие отношение к информатике из слов: лето, петарда, ниша, корвет, иголка, стрелка.
Для передачи информации между компьютерами используются двоичные цифры (единица или ноль). Сколько раз подряд надо передать каждую цифру с учетом редкого возникновения ошибок, чтобы: 1) обнаружить ошибку; 2) исправить её без повторной передачи?
В некоторой стране автомобильный номер длиной 7 символов составляют из заглавных букв (задействовано 23 различные буквы) и десятичных цифр в любом порядке.Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов). Определите объём памяти, отводимый этой программой для записи 50 номеров.
?
```
	
```

Использованная литература

(Не надо смеяться, что мы - не маленькие и нам не надо учиться на вопросах 2 класса: сначала решите все без затруднений! А авторы заданий вполне заслужили моё уважение, так как помогли понять, кто как думает и как кому помочь.)

Приведенную ниже литературу можно использовать и для подготовки к олимпиадам по математике, но, наверняка потребуется помощь учителя.

Знаком * помечены важнейшие книги для самостоятельной работы.

Левитас Г.Г. Нестандартные задачи на уроках математики во втором классе. М.: Илекса, 2006, 52 с.
Левитас Г.Г. Нестандартные задачи на уроках математики в третьем классе. М.: Илекса, 2005, 60 с.
Левитас Г.Г. Нестандартные задачи на уроках математики в четвертом классе. М.: Илекса, 2005, 72 с.
Райан С. Хитроумные математические головоломки / Пер. с англ. М.: АСТ: Астрель, 2005, 92 с.
*Шарыгин И.Ф. Задачи на смекалку: учеб. пособие для 5-6 кл. общеобразоват. учреждений. М.: Просвещение, 2006, 95 с.
*Босова Л.Л. Занимательные задачи по информатике. М.: Бином, 2007, 119 с.
Босова Л.Л. Учебники и рабочие тетради по информатике для 5-7 класса...
Материалы ГИА и ЕГЭ (не надо удивляться).
Смыкалова Е.В. Дополнительные главы по математике для учащихся 5 класса.
*Смыкалова Е.В. Дополнительные главы по математике для учащихся 6 класса. СПб.: СМИО Пресс, 2006, 48 с.
Смыкалова Е.В. Дополнительные главы по математике для учащихся 7 класса.
Мой мозг

Некоторые полезные ресурсы

Всероссийский конкурс «Кит — компьютеры, информатика, технологии».
Готовятся...

Copyright © 1993–2024 Мацкявичюс Д.А. Все права защищены.
Никакая часть сайта не может быть воспроизведена никаким способом без письменного разрешения правообладателя и явной ссылки на данный ресурс.
Медаль выдана сайту гимназии 1549 г.Москвы, в значительной степени состоявшему из представленных здесь авторских материалов

Медаль выдана сайту гимназии 1549 г.Москвы, в значительной степени состоявшему из представленных здесь авторских материалов

Горячие блюда	Напитки
Каша — 40 руб.	Чай — 5 руб.
Омлет — 50 руб.	Какао — 20 руб.
Блинчики — 60 руб.	Кофе — 30 руб..

	1994

		1991