Алгебра логики
Алгебра логики — раздел математики, изучающий высказывания с точки зрения их логических значений (истинности или ложности) и логических операций над ними.
Иногда ее называют двоичной логикой или булевой алгеброй по имени английского математика Джорджа Буля.
Для удобства записи, используют обозначение результата через F, а логические высказывания через A (X) и B (Y). Так как возможных вариантов значений всего два, их можно обозначить через 0 (ложь, нет, false, no) и 1 (истина, да, true, yes).
Таблица истинности — табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Логическое высказывание
Логическое высказывание — любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Примеры
Тождественно истинные высказывания (тавтология)
Тождественно истинными называются высказывания, истинные при любых значениях входящих в него переменных.
Таким образом, такое высказывание всегда равно 1.
В качестве примеров можно привести высказывания, являющиеся разъяснением термина на основе его словообразования (авиабаза — место базирования авиационной техники). Или любое сложное высказывание, смысл которого сводится к формуле А \/ ¬A.
Тождественно ложные высказывания
Тождественно ложными называются высказывания, ложные при любых значениях входящих в него переменных.
Таким образом, такое высказывание всегда равно 0.
Важно, что большинство высказываний сводится к формуле А /\ ¬A.
Эквивалентные высказывания
Эквивалентными (тождественными или равносильными) называются высказывания, значения которых совпадают при любых значениях входящих в него переменных.
Логические операции
Все логические операции могут быть разделены на (в квадратных скобках приведены альтернативные варианты обозначения):
- логическое умножение (конъюнкция или логическое И) [AND, &, /\];
- логическое сложение (дизъюнкция или логическое ИЛИ) [OR, |, \/];
- логическое отрицание (инверсия или логическое НЕ) [NOT, ¬,
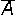 ];
];
- логическое следование (импликация) [→];
- логическое равенство (эквивалентность) [↔, ~].
Логическое умножение (конъюнкция)
Представляет собой объединение нескольких логических выражений с помощью союза И. При практическом наборе на компьютере часто используют знаки прямого и обратного деления без пробела: /\.
Таким образом, все значения должны быть истинными: И первое, И второе, И... При умножении логических операторов мы получим единицу, только если все они будут равны единице:
| A | B | F = A & B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Отсюда вытекает обратное следствие, упрощающее вычисления для конъюнкции:
Если хотя бы одно значение ложно, то ложно и всё выражение.
Логическое сложение (дизъюнкция)
Представляет собой объединение логических выражений с помощью союза ИЛИ. Если при сложении результат становится больше нуля, то он выражается единицей. При практическом наборе на компьютере часто используют знаки обратного и прямого деления без пробела: \/
| A | B | F = A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда вытекает обратное следствие, упрощающее вычисления для дизъюнкции:
Если хотя бы одно значение истинно, то истинно и всё выражение.
Логическое отрицание (инверсия)
Представляет собой логическое выражение с добавленной в начале частицей НЕ. То есть операция всегда обращает значение в противоположное.
| A | F = ¬A |
| 0 | 1 |
| 1 | 0 |
Логическое следование (импликация)
Связывает два логических выражения с помощью оборота ЕСЛИ..., ТО.
Дополнительная операция, так как A → B = ![]() \/ B
\/ B
Кроме того, при построении высказывания могут использоваться выражения «из... следует», «... влечет».
| A | B | F = A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
В таблице хорошо видна практическая суть: импликация ложна только тогда, когда первое выражение истинно, а второе ложно.
При решении задач, в большинстве случаев требуется применение закона снятия импликации.
Логическое равенство (эквивалентность)
Образуется соединением двух логических выражений с помощью оборотов «тогда и только тогда», «необходимо и достаточно», «...равносильно...».
Поскольку мы видим здесь двойное следование (и вправо и влево), операцию иногда называют двойной импликацией.
Дополнительная операция, так как A ↔ B = (A ∨ ![]() ) & (
) & (![]() ∨ B)
∨ B)
| A | B | F = A ↔ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Суть: эквивалентность ложна только тогда, когда выражения разные.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
Порядок решения логического выражения
В первую очередь надо учитывать, что порядок задается скобками.
Далее выполняются операции отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности.
Построение таблиц истинности
Чтобы решить логическое выражение, необходимо построить таблицу истинности, описывающую ВСЕ возможные варианты значений переменных величин. В связи с тем, что мы используем булевы переменные (то есть имеющие только два значения: 0 и 1), количество вариантов легко сосчитать по формулеM = 2N,
где N — число переменных, а M — число строк в результирующей таблице.Заполнение же значений фактически является последовательным вписыванием в каждой строке двоичных чисел. Для первой строки это будет 0 (00, 000...), для второй — 1 (01, 001...), а для последней — числа, состоящего из всех единиц. Выполнение этого несложного правила позволит не только избежать ошибок, но и облегчит решение, так как значения 0/1 будут подчиняться определенному порядку для каждой переменной.
Графическое решение числовых выражений по координатной прямой
Ряд заданий в алгебре логики основывается в использовании в качестве высказывания числового выражения. Например,
(X > 2) /\ ¬(X > 5).
Хорошо видно, что выражение берется в скобки для однозначного восприятия. Прежде чем наносить значения на рисунок, следует избавиться от отрицания. В этом случае происходит замена знаков отношения на противоположные по схеме: < ↔ ≥, > ↔ ≤, = ↔ ≠.
В нашем примере мы получим
(X > 2) /\ (X ≤ 5).
Нанесем два значения на координатную прямую и, учитывая логическое И, у нас должны совпасть оба условия. То есть на прямой это будет пересечение, обозначенное красным.
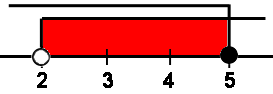
Возможные целочисленные ответы — 3, 4, 5.
Построение логического выражения по таблице истинности
Задача является противоположной стандартной.
При ее решении нужно построить дизъюнкцию для всех строк, равных 1, то есть составить выражение в дизъюнктивной нормальной форме (ДНФ).
Решение текстовых задач
На предыдущих этапах, в частности, изучались графический и табличный способы, которые невозможно, либо чрезмерно трудоемко использовать для сложных заданий. Также, решение задач путем рассуждений зачастую неэффективно.
Многие учащиеся очень расстраиваются, что, используя ранее эти способы, они тратили много времени на то, чтобы выработать стратегию, правильно понимать задание и т.п. А теперь их удается решить буквально за несколько секунд. Эта позиция неверна. Большинство подобных задач в реальной жизни не содержит достаточных сведений для решения средствами алгебры логики. Умение анализировать данные и находить «пробелы» в исходных данных — намного важнее.
При решении логической задачи средствами алгебры логики, необходимо выделить из текста логические условия и записать их в виде выражения.
Каждое высказывание оформляется в виде логической переменной. Чаще всего удобно вводить переменные, обозначенные русскими буквами и связанные с объектами, описанными в задаче: Иван — И, красный — К (или Кр, если переменная К уже введена для Коли) и т.п.
Соотношение переменных определяется связывающими высказываниями.
- И, ИЛИ, НЕ.
- «из... следует»; «... влечет»; ЕСЛИ..., ТО (импликация)
- «тогда и только тогда», «необходимо и достаточно», «...равносильно...» (эквивалентность).
В большинстве случаев потребуется упрощение выражения с использованием законов алгебры логики.
В некоторых случаях удобно составить систему высказываний (аналогично системе уравнений) и, затем, решать уже её.
Логическое значение категорически рекомендуется записывать как 0 (ложь) или 1 (истина). Это поможет дифференцировать записи, а не спотыкаться о глупейшие варианты Л/И.
Трое друзей поспорили о результатах предстоящих скачек. Иван: Ласточка не придет первой, первой будет Стрела. Сергей: Победит Ласточка, а Тормозу ни за что не быть первым. Петр: Стреле не видать первого места, а Тормоз готовился очень тщательно. По итогам скачек оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего оказались ошибочными. Кто выиграл этап гонки? |
Введем обозначения для логических высказываний:
Л — победит Ласточка; С — победит Стрела; Т — победит Тормоз.
Запишем высказывания (высказывание Петра "Тормоз готовился очень тщательно" не содержит информации о месте и не может быть учтено):
1) ¬Л /\ С, 2) Л /\ ¬Т, 3) ¬С.
Учитывая истинность предположений двух друзей и ложность третьего, запишем истинное высказывание, основанное на том, что неправ либо первый, либо второй, либо третий:
[(¬Л /\ С) /\ (Л /\ ¬Т) /\ ¬¬С] \/
\/ [¬(¬Л /\ С) /\ ¬(Л /\ ¬Т) /\ ¬С]
\/
\/ [¬(¬Л /\ С) /\ (Л /\ ¬Т) /\ ¬С] = 1
Затем упростим его за счет двойного отрицания, правила Моргана и убрав ненужные для первого члена скобки:
[¬Л /\ С /\ Л /\ ¬Т /\ С] \/ [(Л \/ ¬С) /\ (¬Л \/ Т) /\ ¬С] \/ [(Л \/ ¬С) /\ (Л /\ ¬Т) /\ ¬С] = 1
Выражение по-прежнему немаленькое. Далее, по закону поглощения можно сократить показанное красным
[¬Л /\ С /\ Л /\ ¬Т /\ С] \/ [(Л \/ ¬С) /\ (¬Л \/ Т) /\ ¬С] \/ [(Л \/ ¬С) /\ (Л /\ ¬Т) /\ ¬С] = 1
[(¬Л \/ Т) /\ ¬С] \/ [(Л /\ ¬Т) /\ ¬С] = 1
{(¬Л \/ Т) \/ (Л /\ ¬Т)} /\ ¬С = 1
{¬Л \/ Т \/ (Л /\ ¬Т)} /\ ¬С = 1
Здесь
{(Л \/ ¬Л \/ Т) /\ (¬Т \/ ¬Л \/ Т)} /\ ¬С = 1
В оставшейся части сократим противоположные слагаемые (по закону исключения третьего)
Т /\ ¬Л /\ ¬С = 1
Конечно, можно сразу сказать, что в произведении все три множителя должны быть равны единице, то есть: Л = 1, Т = 0, С = 0. Ответ: победителем скачек стала Ласточка.
Но можно сделать то же, построив таблицу истинности:
| Л | Т | С | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Дополнительная литература
- Википедия.
- Логические основы компьютеров.
- Учебник по алгебре логики.
- Лемешев С.В. Решение текстовых задач, 2009.
Вопросы и задачи
- Упростите выражение: (X /\ Y) → ¬Z.
- Найдите решения выражения: ((X → Y) \/ Z) ↔ X.
- Определите истинность выражения: (Z \/ X) → (Y /\ X).
- Определите истинность выражения: ((C \/ B)→B) /\ (A /\ B))→B.
- Упростите выражение: A \/ B \/ (¬A \/ B) \/ C /\ D.
- Упростите выражение: (A \/ B) /\ (A \/ B \/ C).
- Решить в Excel выражение (без его преобразований): F = ¬X /\ ¬Y \/ Z \/ X /\ Y.
- Для какого из названий животных ложно высказывание: ((Заканчивается на согласную букву) /\ (В слове 7 букв) → ¬(Третья буква согласная))?
1) Верблюд 2) Страус 3) Кенгуру 4) Леопард - Какое из приведенных имен удовлетворяет логическому условию
((первая буква гласная → вторая буква гласная) /\ последняя буква гласная)?
1) ИРИНА 2) МАКСИМ 3) АРТЕМ 4) МАРИЯ - Упростите выражение: A /\ B \/ A /\ B /\ (C \/ D).
