Системы счисления для начинающих

Страница появилась в связи с тем, что большинство учителей, извините, не удосуживаются разобрать основы. Между тем (вывод из практики), попытки освоится с темой могут быть как у второкласссника, так и у родителей восьмиклассника.

Приведенная ниже информация является попыткой "разжевать" все необходимые аспекты именно с учетом условно "нулевых" знаний, а не дополнения к материалу занятий, как описано в основном разделе по теме. Из-за этого же многое будет повторяться много раз. Наоборот, часть сведений даже не упоминается.

Почти весь материал посвещен разбору десятичной и двоичной систем счисления.

Внимание! На страницу нет прямой ссылки с сайта и она не будет поддерживаться и развиваться, несмотря на незавершенность! Все исправления вносятся только по ссылке выше. Извините, сменились приоритеты.

Что нужно знать (понимать) до того, как приступать к разбору?

Отсюда вытекает, что изучать материал по системам счисления способен любой, кто освоил умножение. В норме, это конец 2-го — начало 3-го класса.

Для удобства рассуждений неплохо бы знать разделение чисел на разряды и классы, что является тематикой 4 класса в большом числе программ. Пока не хотелось бы переходить на изложение этого материала, так что, в случае необходимости, обратитесь к поисковым системам с запросом "разряды и классы".

Теперь немного основной и упрощенной терминологии.

Основание системы счисления — количество различных символов или знаков, используемых для записи чисел. Основание заложено в название системы счисления, то есть два — для двоичной (0 и 1) и десять — для десятичной (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9). Основание записывается в нижнем индексе после числа: 102 в двоичной, 1010 в десятичной. По общепринятым правилам, все вычисления на всех уроках и в повседневной жизни делаются в десятичной системе, которая при этом никак не указывается, то есть любое число считается десятичным и это никак дополнительно не выделяется. На обычных уроках информатики изучаются двоичная, восмеричная и шестнадцатеричная системы счисления.

Алфавит системы счисления — перечень символов, используемых для записи чисел.

Если для десятичной системы это будут 10 цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а для двоичной — только две (0 и 1). В свою очередь, восмеричная система счисления потребует 8 цифр (0, 1, 2, 3, 4, 5, 6, 7).

Алфавит составляется из арабских цифр, начиная с нуля. Если 10 цифровых знаков не хватает, то добавляются латинские буквы (например, в шестнадцате­ричной системе добавляются A, B, C, D, E и F).

Разрядная цифра — наименьшее число, которое может быть добавлено в данном разряде. С точки зрения систем счисления, разрядные цифры всегда записывают одинаково (единица и сколько-то нулей): 1, 10, 100, 1000... В реальном числе значение может превышать цифру, то есть получатся разрядные слагаемые. Так как в двоичной системе наибольшей цифрой является 1, разрядные цифры становятся единственным вариантом разрядных слагаемых.

(Я заранее предвижу крики математиков, что это не верно, но так нужно, ибо ни они, ни учителя начальной школы ничего не объясняют. На последующем этапе мы можем говорить о том, что разрядную цифру взяли несколко раз, то есть не 30, а 3*10.)

Разрядное слагаемое — цифра, которая записана в конкретном разряде с добавлением к ней необходимого числа нулей. Важно, что предельное значение слагаемого зависит от системы счисления. Так, для второго разряда (десятков) оно составит: 10 в двоичной (00 и 10) и 90 в десятичной (00, 10, 20, 30, 40, 50, 60, 70, 80 и 90).

Для начала, хотелось бы вернуться к увеличению разрядов на примере однозначного числа в привычной десятичной системе.

Будем считать, что изначально число равно нулю. Прибавив к нему единицу, мы получим 1, прибавив еще единицу, получим 2 и так — до достижения максимальной цифры 9 (разряд заполнен до предела).

Если прибавить еще 1, то увеличение цифры становится невозможным (она и так самая большая) и мы можем сказать, что разряд переполняется. В этом случае производится запись единицы в следующем разряде (десятков), а разряд единиц становится равным нулю. Таким образом мы получаем число 10. (9 + 1 = 10.)

Стоп! Именно в этом выражении скрыт один из ключей к работе со всеми системами счисления. Достаточно понять, что первое слагаемое не просто цифра девять, а самая большая цифра для данной (десятичной) системы счисления.

Степени чисел в десятичной системе

Прежде чем приступать к обсуждению. В последние годы изучение данной темы как на информатике, так и на математике почти не обсуждается.

Для освоения систем счисления необходимо четкое и полное понимание использования степеней чисел, которое в курсе математики к моменту проведения первых уроков по системам счисления (зачастую 5–6 класс) изучается недостаточно полно (в лучшем случае, только квадрат и куб).

Несмотря на то, что степень числа может принимать любое значение, нас будет интересовать только натуральные (целые) и нулевая степени на примере десятичной системы.

Степень числа введена в математике для упрощения записи и уменьшения объема этой записи. Ее смысл заключается в том, что, если один и тот же множитель в произведении повторяется несколько раз, то можно записать его один раз и дополнительно указать, сколько его было. То есть 5·5 = 52 (две пятерки), 5·5·5 = 53 (три пятерки). При этом 5 = 51 (одна пятерка). По другому: записываем число, а справа от него и вверху записываем, сколько раз оно умножается само на себя.

Множитель может быть неизвестным (или любым числом) и его можно обозначить буквой, например, a. Тогда предыдущие записи примут вид a2 (a·a), a3 (a·a·a), a1 (a).

Вероятно, чуть выше вы заметили, что любое число в первой степени равно самому себе a1 = a.

· an = [Степень]. Значения степеней, которые могут пригодится, приведены ниже.

Для наших вычислений крайне важно учитывать еще одно правило, . Любое число в нулевой степени равно единице a0 = 1.

Хоть нам это и не понадобится, следует упомянуть, что 0n = 0. То есть возведение нуля в любую степень дает ноль.

Сложение чисел

Первым и наиглавнейшим правилом нужно считать то, что арифметические действия с числами возможны только если они записаны в одной и той же системе счисления. Исключений два: чиса 0 и 1 равны сами себе в любой системе счисления.

Складывать цифры разрядов надо по "давно забытому" правилу: если их сумма меньше предельной цифры (9 для десятичной системы), то их надо просто сложить. Если же сумма превышает эту максимальную цифру, то одно из слагаемых должно быть разложено на две части, одна из которых дополнит второе слагаемое до переполнения разряда (10 для десятичной). Пример: 7 + 6 = (7 + 3) + 3 = 10 + 3 = 13.

Перевод чисел

Данное действие можно считать самым простым из всех, относящихся к системам счисления. Каждая цифра числа образует слагаемое, которое надо записать, а потом произвести необходимые арифметические действия.

Прежде чем перейти к конкретным рассуждениям, надо отметить, что приводимые в заданиях числа, обычно не превышают 102410 или ненамного больше этого значения. Это связано с разумным ограничением сложности вычислений.

Степень0123 45678910
Результат124816 32641282565121024
X2*110100 100010000 ...     
* Несложно заметить, что какая степень, столько нулей записано в двоичном числе.

Любое из производимых действий будет замкнуто на эту таблицу!

В десятичную систему

Вне зависимости от обсуждаемой системы счисления, любое число можно разбить на разряды, каждый из которых вносит определенный вклад в значение числа. Общей закономерностью является то, что чем правее стоит цифра, тем меньшее значение она подразумевает.

В качестве первого примера рассмотрим число 1111n

В двоичной системе (11112), каждая разрядная единица означает наличие в числе соответствующей степени 2, а ноль — её отсутствие.

Конечно, можно разложить число на разрядные слагаемые и перевести их, зная следующее правило: сколько нолей, такая и степень двойки.

11112 = 10002 + 1002 + 102 + 12 = 23 + 22 + 21 + 20 = 8 + 4 + 2 + 1 = 15.

Но можно и не делать такой громоздкой записи, а провести рассуждения от последней цифры. Конечно, важно, что в любой системе счисления она означает именно то, что в ней записано. Но, в данном случае, оно означает 20 = 1. Все последующие цифры означают последующие же степени числа 2.

Таким образом, мы можем сразу записывать, продолжая рассуждать к началу числа:

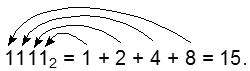
Важно, что не нужно делать никакого подсчета, в каком разряде стоит единица. Просто записываем слагаемые из числового ряда. Если в разряде будет стоять ноль, то мы просто пропустим соответствующее число (4 для следующего примера):

10112 = 1 + 2 + 8 = 11.

В троичной системе (11113), каждая разрядная единица означает наличие в числе соответствующей степени 3. Вот и все отличия. Воспользуемся последним способом перевода, как более эффективным.

11113 = 1 + 3 + 9 + 27 = 40.

Вряд ли на такие расчеты нужно более десятка секунд.

В качестве второго примера рассмотрим число 1234n

Из того, что в числе использована цифра 4 следует, что система счисления, как минимум, пятеричная.

Но теперь не все цифры равны единице. Это всего лишь означает, что соответствующая степень взята не один, а несколько раз:

12345 = 4•50 + 3•51 + 2•52 + 1•53 = 4 + 15 + 50 + 125 = 194.

Короче и доступнее: 12345 = 4 + 3•5 + 2•25 + 1•125 = 4 + 15 + 50 + 125 = 194.

Четверку мы записали по описанному выше правилу, что последняя цифра всегда означает то, что написано.

Для шестеричной системы то же самое, но значение увеличится:

12345 = 4•60 + 3•61 + 2•62 + 1•63 = 4 + 18 + 72 + 216 = 310.

В заключение переведем 16-ричное число:

2AF5 = 15 + 10•16 + 2•256 = 687.

Общая формула для перевода:

@

где m — основание системы счисления, k — номер разряда числа.

Из десятичной системы

1. Остаток от деления

Последовательно делим число на основание до тех пор, пока не получим частное, равное нулю. Остатки записываем. После завершения вычислений записываем значения остатков в обратном порядке. Полученное число и будет ответом.

Разложим два числа: 23 и 64.

ДелимоеОстатокСмысл действия
23
10
5
2
1
0		 1
1
1
0
1
 		 23/2 = 22/2 + 1 = 11 + 1
11/2 = 5 + 1
5/2 = 4/2 + 1 = 2 + 1
2/2 = 1 + 0
1/2 = 0 + 1
 
2310 = 101112
ДелимоеОстатокСмысл действия
64
32
16
8
4
2
1
0		 0
0
0
0
0
0
1

 64/2 = 32 + 0
32/2 = 16 + 0
16/2 = 8 + 0
8/2 = 4 + 0
4/2 = 2 + 0
2/2 = 1 + 0
1/2 = 0 + 1

6410 = 10000002

В некоторых учебниках (например, Босовой) предлагается таблицу записи располагать горизонтально, что очень удобно для сравнительно небольших чисел (<211).

В верхней строке записывается число. Остаток от деления (в нашем случае на 2) записывается под ним, а целая часть частного — в следующей колонке.
Делимое23 1152 1
Остаток11 101
Опять перепишем остатки в обратном порядке:
2310 = 101112

Трудно сказать, насколько комфортно ощущают себя люди, производящие привычное деление столь необычным образом. Лично я испытываю значительный дискомфорт, особенно при переводе не в двоичную систему.

Поэтому, давайте перейдем к другому, менее «магическому» способу.

2. Разложение

Как известно, любое число можно представить в виде суммы чисел.

Запишем значения степеней числа 2:
Степень0123 45678910
Результат124816 32641282565121024

и разложим те же числа. В качестве ответа запишем множители для степеней двойки.

6410 = 1•64 + 0•32 + 0•16 + 0•8 + 0•4 + 0•2 + 0•1 = 10000002

2310 = 1•16 + 0•8 + 1•4 + 1•2 + 1•1 = 101112

Давайте переведем 44 в троичную систему тем же способом.

4410 = 1•27 + 1•9 + 2•3 + 2•1= 11223

Таким образом становиться ясно, что для этих вычислений нужно

Порядок действий на практике

  1. Записываем таблицу степеней данного основания. Как правило, сделать это несложно, так как предлагаемые в заданиях числа небольшие (в пределах 1000), а многие степени оказываются заученными на математике квадратами и кубами. В крайнем случае, нахождение следующей степени можно свести к умножению на основание. Предельное значение, которое надо выписать, должно быть меньше переводимого числа.
  2. Вычесть из числа наибольшую подходящую степень (возможно несколько раз). Получим первую цифру и остаток.
  3. Вычесть из числа следующую степень (возможно несколько раз). Получим вторую цифру и остаток.
  4. То же до исчерпания числа.
  5. Так как слагаемые надо находить от большего к меньшему, переписываем значения в ответ по порядку, если не сделали этого ранее.

Пример 3. Переведем 900 в двоичную систему.

  1. Степени не пишем, так как они ОБЯЗАНЫ быть выучены. Каждая степень может входить в число только ОДИН раз!
  2. 1024 — слишком большое.
  3. 512 вычесть можно: 900 — 1*512 = 388.
  4. 256 вычесть можно: 388 — 1*256 = 132.
  5. 128 вычесть можно: 132 — 1*128 = 4.
  6. 64, 32, 16, 8 не вычитаемы, значит, вместо них будут нули: 0000
  7. 4 вычесть можно: 4 — 1*4 = 0.
  8. 2 и 1 не вычитаемы, значит, вместо них будут нули: 00
  9. Перепишем все вычисления:
    900 = 1*512 + 1*256 + 1*128 + 0*64 + 0*32 + 0*16 + 0*8 + 1*4 + 0*2 + 0*1, или
    900 = 1*29 + 1*28 + 1*27 + 0*26 + 0*25 + 0*24 + 0*23 + 1*22 + 0*21 + 0*20.
  10. Если бы мы вели запись цифр двоичного числа по ходу рассуждений, то ответ был бы давно записан.
  11. Ответ: 900 = 11100001002.

В связи с довольно большой трудоемкостью, данный метод едва ли можно назвать слишком простым для двоичной системы. Но он вполне понятен и, из-за необходимости четкой записи, всегда может быть легко проверен.

В некоторых случаях, когда число очень мало отличается от степени основания, перевод может оказаться значительно более быстрым, чем другие способы.

Например, число 11110112 можно представить в виде 11111112–1002. Семь единиц дают 27–1 (127), а двоичная сотня — 22 (4). Итого 127–4 = 123. (Во много раз быстрее, чем делить или раскладывать на слагаемые!)

Ой, обсуждается же прямо противоположное. Любое число, на единицу меньше степени двойки записывается в двоичной системе как единицы, число которых соответствует этой степени:

3 = 22–1 = 112, 7 = 23–1 = 1112, 15 = 24–1 = 11112,...

Буквально пара слов о системах счисления и математике: сколько в числе нолей в конце, столько раз оно делится без остатка на основание системы.

Степени числа 2
Степень0123 4567891011 12131415161718 1920
Результат1248 16 3264128 256 51210242048 40968192163843276865536131072 262 144524 2881 048 576

Степень
2n

РезультатДвоичное

Нолей
(n–1)

Знаков
(n)

 Значения
(штуки)
20110 10–1 (2=21)
212101 20–3 (4=22)
2241002 30–7 (8=23)
23810003 40–15 (16=24)
2416100004 50–31 (32=25)
25321000005 60–63 (64=26)
266410000006 70–127 (128=27)
27128100000007 80–255 (256=28)
282561000000008 90–511 (512=29)

    Выводы (n — число знаков):
  1. 2n. Зная таблицу степеней, задания можно выполнять во много раз быстрее и с меньшей вероятностью ошибиться.
  2. n-значное двоичное число может иметь 2n значений.
  3. Двоичное число, состоящее из n единиц = 2n — 1.
  4. Чтобы найти число битов, требующихся для описания некоторого количества значений, нужно взять ближайшую степень двойки, которая не меньше числа значений. Степень и будет искомым ответом, а также числом разрядов в двоичном числе.
  5. Каждая единица двоичного числа вносит в него вклад, равный 2 в степени своей позиции от правого края минус 1 (2n–1). Проще это оценивать как 2 в степени количества остальных цифр (нулей) справа.
    То есть, 1002 = 22 (два нуля) = 4, 10002 = 23 (три нуля) = 8...
Copyright © 1993–2023 Мацкявичюс Д.А. Все права защищены.
Никакая часть сайта не может быть воспроизведена никаким способом без письменного разрешения правообладателя и явной ссылки на данный ресурс.