ЕГЭ, вопрос 5: Б. Формальное исполнение линейного алгоритма на естественном языке
Проверяемые элементы содержания по спецификации (2021): Формальное исполнение алгоритма, записанного на естественном языке или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд
Кодификатор 1.6.3/1.1.3. Уровень сложности Б, 1 балл.
Время выполнения — 4 минуты.
Автомат получает на вход два двузначных восьмеричных числа. По этим числам строится новое восьмеричное число по следующим правилам.
1. Вычисляются два восьмеричных числа — сумма старших разрядов заданных чисел и сумма младших разрядов этих чисел.
2. Полученные два восьмеричных числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходные числа: 66, 43. Поразрядные суммы: 12, 11. Результат: 1112.
Определите, какое из предложенных чисел может быть результатом работы автомата.
1) 1121; 2) 112; 3) 28; 4) 73.
Что проверяется в этом задании?
- От алгоритмики здесь только способность прочитать и выполнить простейшие (примитивные) действия.
- Запись результатов именно в порядке возрастания, запрещает любые двузначные варианты типа "7"+"3" [см. ответ 4].
- Тупое умение складывать цифры! в восьмеричной системе счисления.
- Понимание, что максимальная цифра может быть только 7 [см. ответ 3].
- Понимание, что максимальная сумма может быть только 7+7 = 16 [см. ответ 1, вторая половинка равна 21].
- Понимание, что сложение двух старших цифр даст ответ от 2 (1+1) до 16, то есть однозначное или двузначное число.
- Понимание, что сложение двух младших цифр даст ответ от 0 (0+0) до 16, то есть однозначное или двузначное число, но можно получить и ноль.
- Приписывание результатов друг к другу не есть сложение: не 10+10=20, а "10"+"10" = "1010". Напомню, что это действие называется "конкатенация".
Задания
- Демо 2021 (5). Дублирует Демо 2020 (6).
- Демо 2020 (6). На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа еще два разряда по следующему правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает число 97 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
- Демо 2019 (6). На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа еще два разряда по следующему правилу: если N четное, в конец числа (справа) дописывается сначала ноль, а затем единица. В противном случае, если N нечетное, справа дописывается сначала единица, а затем ноль.
Например, двоичная запись 100 числа 4 будет преобразована в 10001, а двоичная запись 111 числа 7 будет преобразована в 11110.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.
Укажите минимальное число R, которое больше 102 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
- Демо 2018 (6). На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа еще два разряда по следующему правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы ее цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
- D2018 (6). На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1001 числа 9 будет преобразована в 100111.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа — результата работы данного алгоритма.
Укажите минимальное число N, для которого результат работы алгоритма будет больше 115. В ответе это число запишите в десятичной системе счисления.
- R2018 (6). На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу: складываются все цифры двоичной записи, если
а) сумма нечетная к числу дописывается 11,
б) сумма четная, дописывается 00. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите такое наименьшее число R, которое превышает 114 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе счисления.
- Демо 2017 (6). Автомат получает на вход трехзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127.
Укажите наименьшее число, в результате обработки которого автомат выдаст число 1711.
- Демо 2016 (6-1). На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа еще два разряда по следующему правилу:
а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите такое наименьшее число N, для которого результат работы алгоритма больше 125. В ответе это число запишите в десятичной системе счисления.
- Демо 2016 (6-2). У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 2,
2. умножь на 5.
Выполняя первую из них, Калькулятор прибавляет к числу на экране 2, а выполняя вторую, умножает его на 5.
Например, программа 2121 — это программа
умножь на 5,
прибавь 2,
умножь на 5,
прибавь 2,
которая преобразует число 1 в число 37.
Запишите порядок команд в программе, которая преобразует число 2 в число 24 и содержит не более четырёх команд. Указывайте лишь номера команд.
- Демо 2015 (6-1). Автомат получает на вход четырехзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также третья и четвертая цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.
Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.
- Демо 2015 (6-2). У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавь 1,
2. умножь на 2.
Первая из них увеличивает число на экране на 1, вторая удваивает его.
Например, 2121 — это программа
умножь на 2
прибавь 1
умножь на 2
прибавь 1,
которая преобразует число 1 в число 7.
Запишите порядок команд в программе преобразования числа 3 в число 63, содержащей не более 8 команд, указывая лишь номера команд. Если таких программ более одной, то запишите любую из них.
- Демо 2014 (B1). У исполнителя Квадратор две команды, которым присвоены номера:
1. возведи в квадрат,
2. прибавь 1.
Первая из них возводит число на экране в квадрат, вторая увеличивает его на 1. Запишите порядок команд в программе, которая преобразует число 1 в число 10 и содержит не более 4 команд. Указывайте лишь номера команд.
(Например, программа 2122 — это программа
прибавь 1,
возведи в квадрат,
прибавь 1,
прибавь 1.
Эта программа преобразует число 3 в число 18.)
- Демо 2013 (A5). Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать).
По этим числам строится новое шестнадцатеричное число по следующим правилам.
1. Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.
Определите, какое из предложенных чисел может быть результатом работы автомата.
1) 9F; 2) 911; 3) 42; 4) 7A.
- Демо 2012 (A5). Автомат получает на вход два трехзначных числа. По этим числам строится новое число по следующим правилам.
1. Вычисляются три числа — сумма старших разрядов заданных трехзначных чисел, сумма средних разрядов этих чисел, сумма младших разрядов.
2. Полученные три числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходные трехзначные числа: 835, 196. Поразрядные суммы: 9, 12, 11. Результат: 12119
Определите, какое из следующих чисел может быть результатом работы автомата.
1) 151303 2) 161410 3) 191615 4) 121613
- Демо 2012 (B2). У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь 1,
2. умножь на 3.
Первая из них увеличивает число на экране на 1, вторая — утраивает его.
Запишите порядок команд в программе преобразования числа 1 в число 22, содержащей не более 5 команд, указывая лишь номера команд. (Например, 21211 — это программа
умножь на 3
прибавь 1
умножь на 3
прибавь 1
прибавь 1,
которая преобразует число 1 в 14.)
(Если таких программ более одной, то запишите любую из них.)
- Демо K-2012 (B5). У исполнителя Увеличитель две команды, которым присвоены номера:
1. прибавь 1,
2. умножь на 4.
Первая из них увеличивает число на экране на 1, вторая умножает его на 4.
Программа для Увеличителя — это последовательность команд.
Сколько есть программ, которые число 3 преобразуют в число 48?
- Демо 2011 (B3). У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
Выполняя первую из них, Калькулятор прибавляет к числу на экране 1, а выполняя вторую, утраивает его. Запишите порядок команд в программе получения из 2 числа 26, содержащей не более 6 команд, указывая лишь номера команд.
(Например, программа 21211 — это программа
умножь на 3
прибавь 1
умножь на 3
прибавь 1
прибавь 1
которая преобразует число 1 в 14.)
- Демо 2010 (B5). Исполнитель Робот ходит по клеткам бесконечной вертикальной клетчатой доски, переходя по одной из команд вверх, вниз, вправо, влево в соседнюю клетку в указанном направлении.
Робот выполнил следующую программу:
влево
вверх
вверх
влево
вниз
вправо
вправо
вправо
Укажите наименьшее возможное число команд в программе, приводящей Робота из той же начальной клетки в ту же конечную.
- Демо 2009 (B5). У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 3
2. умножь на 4
Выполняя первую из них, Калькулятор прибавляет к числу на экране 3, а выполняя вторую, умножает его на 4. Запишите порядок команд в программе получения из числа 3 числа 57, содержащей не более 6 команд, указывая лишь номера команд.
(Например, программа 21211 это программа
умножь на 4
прибавь 3
умножь на 4
прибавь 3
прибавь 3
которая преобразует число 2 в 50.)
- Демо 2008 (A20). Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно, снизу свободно, слева свободно, справа свободно
Цикл
ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
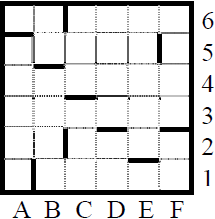
НАЧАЛО
ПОКА < справа свободно > вправо
ПОКА < сверху свободно > вверх
ПОКА < слева свободно > влево
ПОКА < снизу свободно > вниз
КОНЕЦ
1) 1 2) 0 3) 3 4) 4
- Демо 2008 (B3). У исполнителя Утроитель две команды, которым присвоены номера:
1. вычти 2
2. умножь на три
Первая из них уменьшает число на экране на 2, вторая — утраивает его. Запишите порядок команд в программе получения из 11 числа 13, содержащей не более 5 команд, указывая лишь номера команд. (Например, 21211 — это программа:
умножь на три
вычти 2
умножь на три
вычти 2
вычти 2,
которая преобразует число 2 в 8).
(Если таких программ более одной, то запишите любую из них.)
- т2-2012/1 (A5). Определите, какое из предложенных чисел может быть результатом работы автомата.
1) 1121 2) 112 3) 28 4) 73
- т2-2012/2 (A5). Определите, какое из предложенных чисел может быть результатом работы автомата.
1) 27 2) 112 3) 129 4) 2111
- vk_1029a.
Пятизначное число формируется из цифр 0, 1, 2, 3, 4, 5. Известно, что число нечетное и, помимо этого, сформировано по следующим правилам:
а) при делении данного числа на 3 в остатке получается 0;
б) цифра самого младшего разряда на 1 больше цифры в самом старшем разряде.
Какое из следующих чисел удовлетворяет всем приведенным условиям?
1) 40005 2) 51234 3) 11203 4) 41215
- vk_1029b.
Люба забыла пароль для запуска компьютера, но помнила алгоритм его получения из символов «QWER3QWER1» в строке подсказки. Если все последовательности символов «QWER» заменить на «QQ», а из получившейся строки удалить сочетания символов «3Q», то полученная последовательность и будет паролем:
1) 3QQQ1 2) QQ1 3) QQQ 4) QQQ1
- с114 (6). Автомат получает на вход трехзначное число. По этому числу строится новое число по следующим правилам.
1. Перемножаются отдельно первая и вторая цифры, а также — вторая и третья цифры.
2. Полученные два числа записываются друг за другом в порядке невозрастания без разделителей.
Пример. Исходное число: 179. Произведения: 1*7 = 7; 7*9 = 63. Результат: 637.
Укажите наименьшее число, при обработке которого автомат выдает результат 123.
- с124 (6). Автомат получает на вход трехзначное число. По этому числу строится новое число по следующим правилам.
1. Перемножаются отдельно первая и вторая цифры, а также вторая и третья цифры.
2. Полученные два числа записываются друг за другом в порядке невозрастания без разделителей.
Пример. Исходное число: 179. Произведения: 1*7 = 7; 7*9 = 63. Результат: 637.
Укажите наименьшее число, при обработке которого автомат выдает результат 205.
- с112 (6). У исполнителя Калькулятор1 две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 5
Выполняя первую из них, Калькулятор1 прибавляет к числу на экране 1, а выполняя вторую, умножает это число на 5.
Программа для этого исполнителя — это последовательность номеров команд. Например, программа 121 задаёт такую последовательность команд:
прибавь 1
умножь на 5
прибавь 1
Эта программа преобразует, например, число 7 в число 41.
Запишите в ответе программу, которая содержит не более шести команд и переводит число 3 в число 506.
- с122 (6). У исполнителя Калькулятор1 две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 5
Выполняя первую из них, Калькулятор1 прибавляет к числу на экране 1, а выполняя вторую, умножает это число на 5.
Программа для этого исполнителя — это последовательность номеров команд. Например, программа 121 задаёт такую последовательность команд:
прибавь 1
умножь на 5
прибавь 1
Эта программа преобразует, например, число 7 в число 41.
Запишите в ответе программу, которая содержит не более шести команд и переводит число 1 в число 77.
- с113 (6). Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, а также вторая и третья цифры.
2. Полученные два числа записываются друг за другом в порядке невозрастания без разделителей.
Пример. Исходное число: 179. Суммы: 1 + 7 = 8; 7 + 9 = 16. Результат: 168.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 112.
- с123 (6). Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, а также вторая и третья цифры.
2. Полученные два числа записываются друг за другом в порядке невозрастания без разделителей.
Пример. Исходное число: 179. Суммы: 1 + 7 = 8; 7 + 9 = 16. Результат: 168.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 123.
- к112 (6). Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127.
Укажите наименьшее число, в результате обработки которого автомат выдаст число 1412.
- к122 (6). Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127.
Укажите наименьшее число, в результате обработки которого автомат выдаст число 157.
- п111 (6). Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам:
1. Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходное число: 2366. Суммы: 2 + 3 = 5; 6 + 6 = 12. Результат: 512.
Укажите наибольшее число, в результате обработки которого автомат выдаст число 117.
- п121 (6). У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавь 1,
2. умножь на 2.
Первая из них увеличивает число на экране на 1, вторая удваивает его.
Например, 2122 — это программа
умножь на 2
прибавь 1
умножь на 2
умножь на 2,
которая преобразует число 1 в число 12.
Запишите порядок команд в программе преобразования числа 4 в число 57, содержащей не более 7 команд, указывая лишь номера команд. Если таких программ более одной, то запишите любую из них.
- ш115 (6). Автомат получает на вход нечётное число X. По этому числу строится трёхзначное число Y по следующим правилам.
1. Первая цифра числа Y (разряд сотен) — остаток от деления X на 4.
2. Вторая цифра числа Y (разряд десятков) — остаток от деления X на 3.
3. Третья цифра числа Y (разряд единиц) — остаток от деления X на 2.
Пример. Исходное число: 63179. Остаток от деления на 4 равен 3; остаток от деления на 3 равен 2; остаток от деления на 2 равен 1. Результат работы автомата: 321.
Укажите наименьшее двузначное число, при обработке которого автомат выдаёт результат 101.
- ш125 (6). Автомат получает на вход нечётное число X. По этому числу строится трёхзначное число Y по следующим правилам.
1. Первая цифра числа Y (разряд сотен) — остаток от деления X на 4.
2. Вторая цифра числа Y (разряд десятков) — остаток от деления X на 3.
3. Третья цифра числа Y (разряд единиц) — остаток от деления X на 2.
Пример. Исходное число: 63179. Остаток от деления на 4 равен 3; остаток от деления на 3 равен 2; остаток от деления на 2 равен 1. Результат работы автомата: 321.
Укажите наименьшее двузначное число, при обработке которого автомат выдаёт результат 301.
- ш114 (6). Автомат получает на вход четырёхзначное десятичное число, в котором все цифры нечётные. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также третья и четвёртая цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания (без разделителей).
Пример. Исходное число: 7511. Суммы: 7 + 5 = 12; 1 + 1 = 2. Результат: 212.
Сколько существует чисел, в результате обработки которых автомат выдаст число 616?
- ш124 (6). Автомат получает на вход четырёхзначное десятичное число, в котором все цифры нечётные. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также третья и четвёртая цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания (без разделителей).
Пример. Исходное число: 7511. Суммы: 7+5 = 12; 1+1 = 2. Результат: 212.
Сколько существует чисел, в результате обработки которых автомат выдаст число 414?
- ш113 (6). Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, вторая и третья цифры, а также третья и четвёртая цифры. 2. Из полученных трёх чисел выбираются два наибольших и записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 9575. Суммы: 9 + 5 = 14; 5 + 7 = 12; 7 + 5 = 12.
Наибольшие суммы: 14, 12. Результат: 1214.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 1517.
- ш123 (6). Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, вторая и третья цифры, а также третья и четвёртая цифры. 2. Из полученных трёх чисел выбираются два наибольших и записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 9575. Суммы: 9 + 5 = 14; 5 + 7 = 12; 7 + 5 = 12.
Наибольшие суммы: 14, 12. Результат: 1214.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 1418.
- ш112 (6). Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, вторая и третья цифры, а также третья и четвёртая цифры.
2. Из полученных трёх чисел выбираются два наибольших и записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 9575. Суммы: 9 + 5 = 14; 5 + 7 = 12; 7 + 5 = 12.
Наибольшие суммы: 14, 12. Результат: 1214.
Укажите наибольшее число, при обработке которого автомат выдаёт результат 1515.
- ш122 (6). Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, вторая и третья цифры, а также третья и четвёртая цифры.
2. Из полученных трёх чисел выбираются два наибольших и записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 9575. Суммы: 9 + 5 = 14; 5 + 7 = 12; 7 + 5 = 12.
Наибольшие суммы: 14, 12. Результат: 1214.
Укажите наибольшее число, при обработке которого автомат выдаёт результат 1517.
- ш111 (6). Автомат получает на вход пятизначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая, третья и пятая цифры, а также вторая и четвёртая цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 63 179. Суммы: 6 + 1 + 9 = 16; 3 + 7 = 10. Результат: 1016.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 621.
- ш121 (6). Автомат получает на вход пятизначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая, третья и пятая цифры, а также вторая и четвёртая цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 63 179. Суммы: 6 + 1 + 9 = 16; 3 + 7 = 10. Результат: 1016.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 723.
- п115 (6).
- п125 (6).
- п114 (6).
- п124 (6).
- п113 (6).
- п123 (6).
- п112 (6).
- п122 (6).
