Невозможность исчерпывающего алгоритма
Первичная предпосылка: даже для сравнительно простого алгоритма невозможно сформулировать последовательность действий без введения условий (ограничений), порой весьма существенных. Сразу оговорюсь, что речь идет не о простейших (элементарных) алгоритмах, так горячо любимых нашей системой образования и, чаще всего, не имеющих никакого прикладного смысла.
В качестве примера мы возьмем пересечение проезжей части по пешеходному переходу: один из «всем известных» и ежегодно обсуждаемых в школе вопросов.
Традиционная точка зрения
"Посмотреть налево, потом направо. Если поблизости нет едущих машин — перейти". Алгоритм с небольшим развитием рассуждений:
Вспомнив и интерпретировав п.4.6 правил дорожного движения (ПДД): «остановиться на линии, разделяющей транспортные потоки противоположных направлений», можно разбить алгоритм на две части дороги (и это не лишено смысла):
Все. Дальше этого никто двинуться не готов. Это не мои фантазии, это проверенный на многих сотнях школьников результат «просветительской работы» со стороны учителей и сотрудников ГИБДД. Скорее всего, большинство читателей даже не заметили никакого подвоха и пока не понимают к чему поведут рассуждения.
Давайте начнем с того, для чего вообще поднимается эта тема. Подоплека скрыта в безопасности и большом количестве ДТП на пешеходных переходах. То есть, краткий смысл можно сформулировать следующим образом: как не попасть под машину, переходя дорогу по правилам?
Обратимся к ПДД.
4.5. На нерегулируемых пешеходных переходах пешеходы могут выходить на проезжую часть (трамвайные пути) после того, как оценят расстояние до приближающихся транспортных средств, их скорость и убедятся, что переход будет для них безопасен...
14.1. Водитель транспортного средства, приближающегося к нерегулируемому пешеходному переходу, обязан уступить дорогу пешеходам, переходящим дорогу или вступившим на проезжую часть (трамвайные пути) для осуществления перехода.
Отсюда вытекает не только преимущество пешехода, но и его обязанность убедиться в безопасности. Алгоритм существенно меняется.
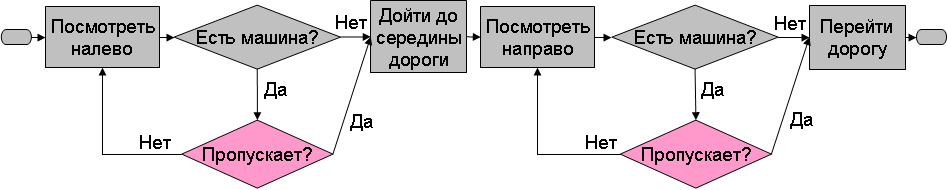
Без внесения изменений в блок-схему, оговорим, что полос в одном направлении может быть несколько и каждую из них надо оценивать отдельно. И именно тогда имеет смысл практическое обсуждение разделительной линии.
Все вышесказанное усугубляется оценкой скорости движения транспорта.
А если притормаживающий водитель вдруг решит «проскочить», то есть немножко нарушить правила? Немножко потому что зачастую это совершенно безопасно и не задержит переходящего дорогу. Пешеход должен быть готов и к этому.
Наконец весь уже созданный алгоритм может быть разрушен выездом на встречную полосу транспорта, движущегося справа. И неважно, что будет причиной: отвлечение водителя, неисправность, помеха на дороге, опьянение или что-то другое. Переходя первую часть дороги надо смотреть и налево и направо. Если думаете, что справитесь, то попробуйте изобразить это, запасясь листом бумаги побольше.
А еще есть велосипедисты и мотоциклисты, падающие деревья, скользкая поверхность и т.д., до бесконечности. Сколь бы маловероятным все это не казалось, оно есть, увеличивает риск и должно присутствовать в полном алгоритме. Например, написанном для робота...
Итак, при построении блок-схемы «на все случаи жизни» нам вряд ли удасться уложиться в лист формата А0, а следование «урезанным» вариантам всегда сопряжено с определенной степенью риска.
Заметьте, что мы даже не упоминаем регулируемый переход, проезд спецтранспорта и неположенные места. Но думается рассуждения по этому поводу можно построить самостоятельно :)
Стоит ли тогда заниматься построением заведомо несовершенных алгоритмов? Безусловно да! Необходимо лишь оговаривать укрупнение и опускание отдельных моментов, обосновывание их малой значимости.
Copyright © 1993–2024 Мацкявичюс Д.А. Все права защищены.
Никакая часть сайта не может быть воспроизведена никаким способом без письменного разрешения правообладателя и явной ссылки на данный ресурс.
